Better Synthetic Data with Redpoll Reformer
Complex artificial data creation that maintains meaning
2021-10-13 by Bryan Dannowitz in [ai, data, anonymization, synthetic data]
NOTE: This post was written using an early, and now deprecated, version of Redpoll software. The API has changed, but the concepts are the same.
Oftentimes data is a scarce resource or difficult to share. Data-hungry models may require more data than we have, and data sensitivity issues may prevent us from sharing data externally — or even internally — which prevents us from fully realizing the value of our data. One solution is to generate synthetic data. If we have a generator that can create data that have the same statistical properties as an input data set, we can synthesize as many secure data as we like. But synthesizing data is a knotty task. Important data are often complex, containing many variables with complex interactions, errors, and anomalies. Thus a great deal of work, and no small number of AI companies, have been dedicated to developing frameworks to generate convincing synthetic data.
Here, we explain:
- Why one might wish to generate synthetic data
- How current state-of-the-art methods for data synthesis work
- Evaluation methods for the quality of synthetic data
- How the Redpoll Reformer Engine can provide higher quality synthetic data than state-of-the-art
Contents
- Why Synthetic Data
- Generating Synthetic Data
- Evaluating Generated Data
- Better Synthetic Data With Reformer
Why Synthetic Data
It's a common perception that vast torrents of data are ubiquitous and readily available -- but that's not always the case. Specific scenarios exist that might make data scarce or inhibit usability:
- The desired data is scarce, or expensive to collect and label
- The data in hand is imbalanced, and you want a balanced set
- There are privacy concerns with using the existing data
This last item can be a significant limiting factor for many seeking to perform data analysis.
Let's say that you work for a health insurance provider. There are warehouses of data that have been painstakingly collected, aggregated, cleaned, and housed. Actionable information and predictive power exists in that stockpile! However, it is an unwarranted vulnerability to make this raw data available to every analyst and data scientist on staff. All of that personal information dispersed about the company is a vast HIPAA incident waiting to happen.
Besides the trivial solution of simply removing a prescribed selection of features (the "safe harbor" de-identification standard)), generating synthetic data is an practical approach to opening up usage of the information that the original data contains.
The trick is for the new dataset to retain nearly identical distributions and dependencies (information). If data were generated in this way, it may be shared and used freely. But (!) one must also check that there is a low risk of real samples frequently occurring in the new dataset, which would throw the privacy benefits of synthetic data out the window.
Generating Synthetic Data
Broadly speaking, all one needs to do to generate synthetic data is to learn the joint probability distributions of all the features in the dataset. This, however, becomes more and more difficult when:
- There are many features that all depend on each other
- There is not much data to learn these joint distributions from
- The individual distributions are irregular
- The features are of varying types (categorical, ordinal, numeric, missing)
With enough information, one can rely on deep learning approaches such as Variational Auto-Encoders (VAE) and Generative Adversarial Networks (GAN). A VAE encodes data into a latent space, and then reconstructs them, tuning their encoder-decoder networks to minimize reconstruction error. A GAN turns random noise into a synthetic sample. The GAN then trains a discriminator to distinguish between real and synthetic samples and then tunes the generator to make more effective samples. This back and forth effectively induces an arms race of improvement. The discriminator finds weaknesses in the generator, and the generator must improve to overcome them, thereby becoming more effective.
These have proven to be very effective at specific tasks, especially in the realm of imagery, but they can also be very finicky to work with, often requiring considerable expertise just to get operational. Some considerations:
- GANs need to be given a good initial state to work.
- It can be challenging to tell when to stop training them.
- GANs are prone to mode collapse phenomenon -- produces one or few modes of synthetic samples that work; not the desired variety
- VAEs prove difficult in defining reconstruction error for heterogeneous data (different data types, scales)
Another approach is to commit to a modeling approach whose focus is to actually learn these individual and joint distributions -- not to mimic them through black box trial and error. We'll discuss more on this and Redpoll's Reformer platform after we discuss how to evaluate synthetic data.
Tabular GAN-generated Data
For this demo, we will be using the Heart Disease Dataset from the UC Irvine Machine Learning Dataset Repository. It is relatively small with mixed data types, and a non-trivial prediction target (i.e. typical model performance is in the 80%'s, not the 99.9%'s).
| id | age | sex | chest_pain_type | blood_pressure | cholesterol | ... | resting_ecg | max_heart_rate | heart_disease_diagnosis |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 55 | M | asympt | 140 | 217 | ... | normal | 111 | True |
| 1 | 65 | M | typ_ang | 138 | 282 | ... | hypertrophy | 174 | True |
| 2 | 45 | F | atyp_ang | 130 | 234 | ... | hypertrophy | 175 | False |
| 3 | 56 | F | asympt | 200 | 288 | ... | hypertrophy | 133 | True |
| 4 | 54 | M | asympt | 110 | 239 | ... | normal | 126 | True |
Most GAN architectures are geared towards image features. Still, the ctgan package uses an architecture based on the GAN-based Deep Learning data synthesizer, the paper Modeling Tabular data using Conditional GAN (PDF) presented at the NeurIPS 2019 conference. With it, one can train the network and generate new data by running something like:
import pandas as pd
from sklearn.model_selection import train_test_split
from ctgan.synthesizers import CTGANSynthesizer
# Load data, splitting into features and target
hd_df = pd.read_csv("heart_disease.csv", index_col=0)
X_hd = hd_df.iloc[:, :-1].copy()
y_hd = hd_df.iloc[:, -1].copy()
# Simulate based on a subset (train) of the full data set
X_hd_train, X_hd_test, y_hd_train, y_hd_test = train_test_split(
X_hd, y_hd, test_size=0.33, random_state=42
)
# Anything with discretized values needs to be explicitly identified
discrete_columns = (
'sex',
'chest_pain_type',
'fasting_blood_sugar_gt120mg',
'resting_ecg',
'exercise_induced_angina',
'heart_disease_diagnosis',
)
# Instantiate the synthetic data generator
ct_hd_gen = CTGANSynthesizer(epochs=2000)
# Train the GAN on the training data
ct_hd_gen.fit(
pd.concat([X_hd_train, y_hd_train], axis=1),
discrete_columns=discrete_columns
)
# Generate a sample the same size as the real training set
ct_hd_df = ct_hd_gen.sample(len(X_hd_train))
# Split into features and target
ct_hd_train = ct_hd_df.iloc[:, :-1]
ct_hd_target = ct_hd_df.iloc[:, -1]
After training for a while, a new training set and corresponding targets will be generated that, to the eye, looks to be the real deal! But how does one know if it's really any good?
Evaluating Generated Data
There are several approaches one can take to evaluating a synthetic data set:
- Individual Distributions - do the feature distributions match well between real and synthetic data?
- Joint Distributions - Evaluate and compare correlations between features. This can easily be done between two features.
- Modeling Utility - Compare how effective synthetic data is for training a model to one trained with real data.
- Model Indistinghuishability - Test how well a classifier can distinguish between real and synthetic data.
These evaluations should be enough to get the measure of how similar the real and synthetic datasets are.
Univariate Distributions
A simple check between real and synthetically generated data is to ask whether the individual feature distributions match. These can be quickly inspected by plotting their probability distributions over one another and applying a statistical independence test on them (e.g. Kolmogorov-Smirnov 2-sample test for continuous and chi-squared for discrete).
Above: Distribution plots of real (blue) vs CTGAN synthetic (orange) data for each variable in the data set. KDE plots denote continuous variables; bar plots denote categorical variables. The closer the orange and blue align, the more similar the synthetic and read univariate distribution. Each plot shows the p-value of the test. The p-value indicates the probability that the two data sets came from the same distribution. The lower the p-value, the more dissimilar the datasets.
We see that the continuous GAN-generated distributions are statistically distinguishable, while some discrete ones hit the mark. Perfection here isn't expected; it's encouraging for feature distributions to look so similar.
Joint Distributions
What makes a dataset unique and valuable is its structure, or how different features depend on one another. With the simulated data, how much of the structure is preserved? A quick way to summarize this is by calculating the feature-feature correlations for each of the two datasets and comparing them.
For this, we plot the correlation heatmap between each pair of features. Such a heatmap can be made for the real and synthetic datasets, and then the difference between the two can be calculated. The closer to zero that these differences are, the better the quality.
Above: Correlation plots. Each cell shows the correlation between a pair of variables. Left) Real data. Middle) Synthetic data. Right) Error: Real-Minus synthetic. A higher magnitude indicates higher error.
On the left, you can see the "fingerprint" of the original dataset, with the corresponding correlations observed in the synthetic sample in the middle. While one or two feature-feature correlations are matched, much is missed.
Modeling Utility
To evaluate whether the dataset at hand has the same predictive power, we can set up a straightforward comparison:
- Train model A on the real training set
- Train a separate model B on the synthetic set, which has only learned from the training set
- Evaluate both models on the classification task using the real, held-out test set
If the performance metrics are in the same ballpark with respect to each other, we can rest assured that it's very likely the case that the synthetic set should be suitable for subsequent analysis and modeling.
We start by seeing what performance one can expect by using the real data. The choice of a classifier isn't too important, as long as it would be able to pick up on any differences.
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import average_precision_score, roc_auc_score, accuracy_score
# Train the model and get prediction scores
rfc = RandomForestClassifier().fit(X_hd_train, y_hd_train)
y_pred = rfc.predict_proba(X_hd_test)[:, 1]
This simple scenario evaluates to the following metrics:
test_accuracy : 0.811
test_roc_auc : 0.859
test_average_precision : 0.860
We follow that by training on our generated samples and assessing the performance on the real test data:
synth_rfc = RandomForestClassifier()
synth_rfc.fit(ct_hd_train, ct_hd_target)
y_pred_synth = synth_rfc.predict_proba(X_hd_test)[:, 1]
test_accuracy : 0.774
test_roc_auc : 0.865
test_average_precision : 0.867
We can see that these classifiers are similarly as effective at the classification task, which is what we would hope to see. It should, however, be noted that the performances metrics like accuracy should rarely meet the real data's performance. Some metrics like ROC and PR AUC may end up meeting the baseline, as they do here, but these more summarize the model's ability to order the prediction scores more than they are to score them properly above/below threshold.
This is just a brief example, naming one target feature. If one wished to be very thorough, this procedure could be repeated for each feature in the dataset being treated as the target.
Indistinguishable Data
How similar do the two samples look? Can a discerning classifier do a decent job telling the two apart?
For this test, we apply a real and synthetic label on two equally-sized samples,
mix them up, and see if a machine learning classifier is good at telling them apart.
This trick is typically used to test if your production data has drifted away from
the model's training data, but the method is also applicable here.
We can run this test many times with a binary classifier and plot out the ROC and Precision-Recall curves. Perfect mimicry would be a diagonal line from (0, 0) to (1, 1) on ROC curve, and a horizontal line at (0, 0.5) to (1, 0.5) on the PR curve. For balanced classes, the AUC (area under the curve) would be a value of 0.5 for both. In general, for evaluating such AUC:
- 0.5: Random chance
- 0.6: Poor discrimination
- 0.7: Fair discrimination
- 0.8: Good discrimination
- 0.9: Very good discrimination
- 1.0: Perfect
# Apply a source label to the individual sets
original = hd_df.copy()
original["source"] = 1
simulated = ct_hd_df.copy()
simulated["source"] = 0
# Combine and shuffle them
combined = (
pd.concat([original, simulated])
.sample(frac=1.0)
.reset_index(drop=True)
)
# Use a classifier to perform k-fold cross-validation
rfc = RandomForestClassifier()
res = cross_validate(
estimator=rfc,
X=combined.drop(["source"], axis=1),
y=combined["source"],
scoring=["accuracy", "roc_auc", "average_precision"],
)
# Report results
for val in res:
print(f"{val:>25} : {round(np.mean(res[val]), 3):<03}")
test_accuracy : 0.727
test_roc_auc : 0.804
test_average_precision : 0.807
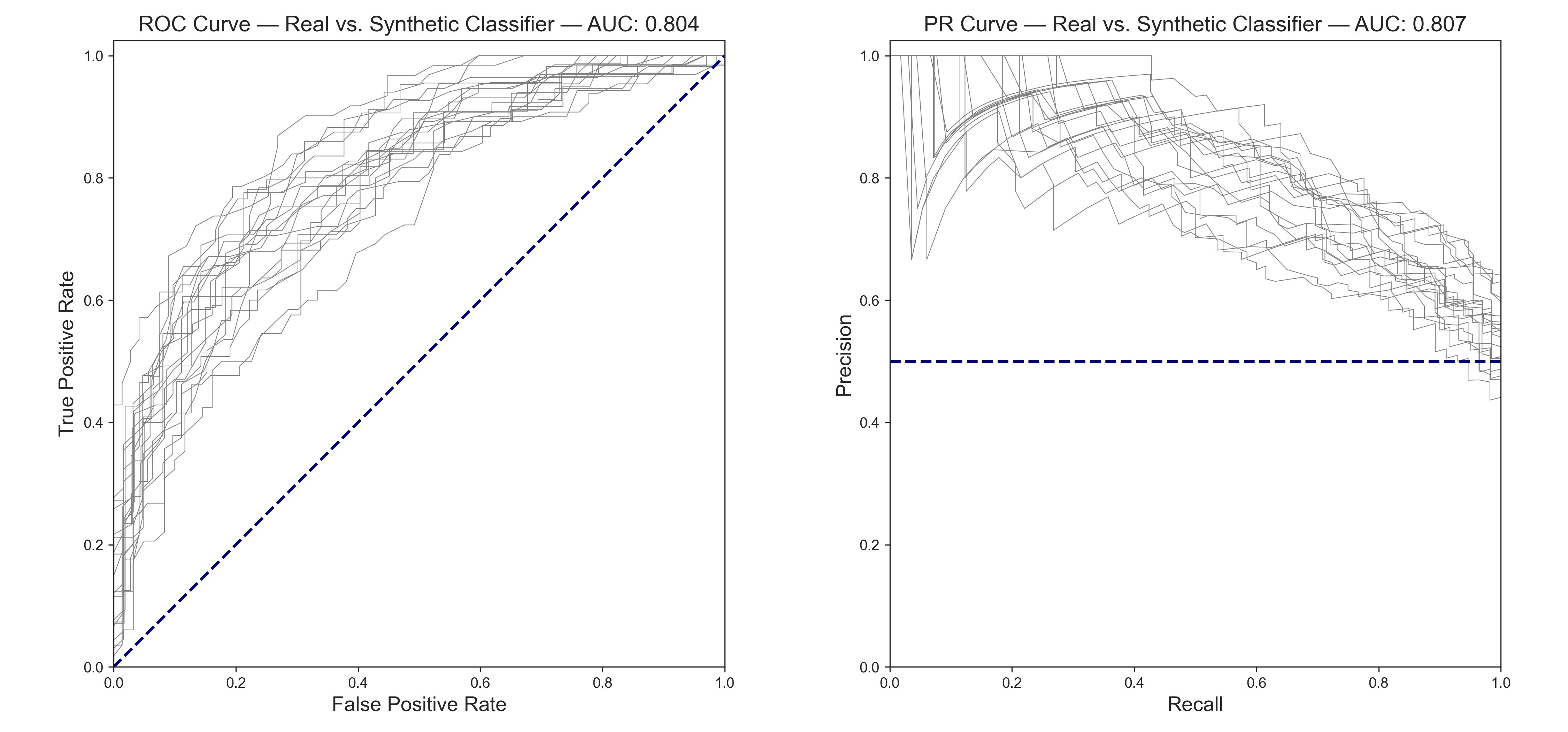
A model can tell the difference between real and CTGAN synthetic data about 70% of the time. This result is okay, as far as synthetic data goes. However, underfitting and generalization are preferred, and there will sometimes be minor quirks in the data that might be a dead giveaway for an aggressive model like the random forest classifier.
But what if we entertain the case that a sneaky, silly "synthetic data generator" just generated copies of real samples? We would see a perfect 0.5 AUC and accuracy, but it still would not be what we want. We want data that's similar, but not at all the same. For this, we must perform an analysis of just how not exactly the same this synthetic dataset is.
Minimum Sample Distance
Privacy is a multi-faceted issue. However, one basic assumption is that if there are synthetic samples that are very similar (or identical!) to real samples, then privacy can be considered to be compromised.
This can be evaluated by transforming all features to numeric values one way or another and calculating the distance from each real sample to every synthetic sample. Then one can collect and plot out the smallest distance value for each real sample.
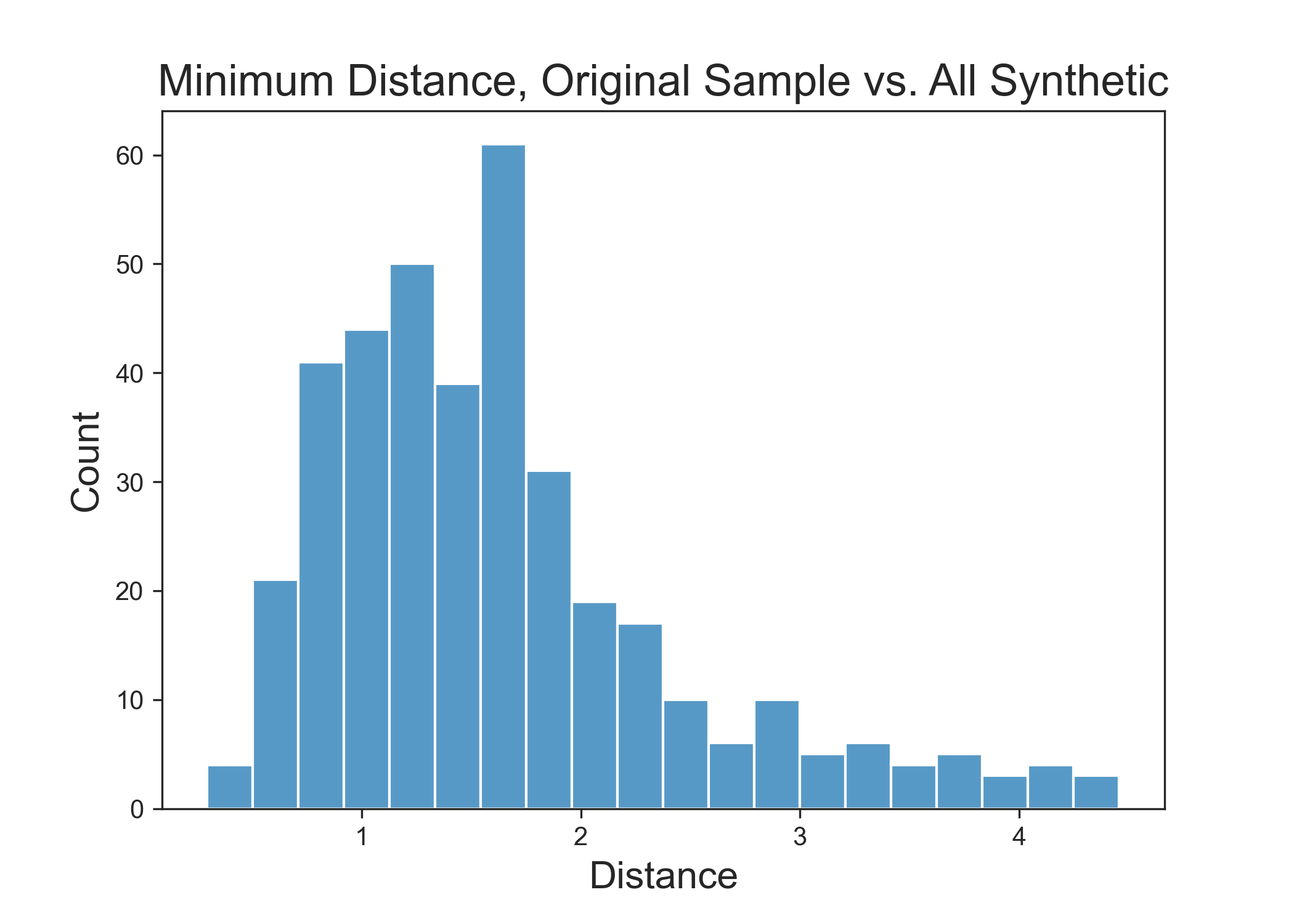
Above: Distance between real data and CTGAN synthetic data. Lower numbers indicate values that are more like the original data. Distance of 0 indicates synthetic data that are identical to real data.
What you are watching for with this plot is a noticeable gap at the near-zero distance value. If there are many samples at or near zero, then this means that are exact samples are being reproduced, which is undesirable behavior. It can occasionally happen by sheer combinatorics, but if it occurs prominently, there's a problem.
What is happening here is that CTGAN did indeed generate samples that are similar to the real data without committing the cardinal sin of exactly reproducing real samples. This type of analysis is critical to perform in these evaluations. If a GAN ever suffered a mode collapse and repeatedly generate real samples, a large bar near zero will reveal the issue immediately.
Note: The absolute distance values will be dataset- and metric-specific. The critical aspect is that there is a gap at the zero end of the range.
Better Synthetic Data With Reformer
Unlike GANs, Redpoll's Reformer Engine is not primarily geared towards generating synthesized data; it is a platform designed to learn the information and joint probabilities of a dataset. It just so happens that, as a side benefit of doing so, one can perform the simulation task for which the GAN and VAE, mentioned above, were designed.
To exhibit Reformer's ability to generate good synthetic data, we can train an engine to learn the structure of the heart disease dataset.
Once this is done, we can simulate as many samples as we want. If we were so inclined, we could simulate
samples given certain feature conditions (say, if we wanted to simulate positive heart disease diagnosis samples).
In this particular case, we will not apply any conditions.
import redpoll as rp
# Run Reformer on the data set
rp.funcs.run('heart_disease.csv', output='heart_disease.rp')
# Start the server (default is on localhost:8000) and connect a client
server_proc = rp.funcs.server('heart_disease.rp')
client = rp.client("0.0.0.0:8000")
# Generate new heart disease data samples
sim_df = client.simulate(col=hd_df.columns, n=len(hd_df))
Let's take a look at the many aspects we inspected before:
Above: Distribution plots of real (orange) vs Reformer synthetic (blue) data for each variable in the data set. KDE plots denote continuous variables; bar plots denote categorical variables. The closer the orange and blue align, the more similar the synthetic and read univariate distribution. Each plot shows the p-value of the test. The p-value indicates the probability that the two data sets came from the same distribution. The lower the p-value, the more dissimilar the datasets.
Here, the univariate distributions match up very well with the real distributions, even to the point that they are, all but age, statistically indistinguishable (p > 0.1).
Above: Correlation plots. Each cell shows the correlation between a pair of variables. Left) Real data. Middle) Reformer synthetic data. Right) Error: Real-Minus synthetic. A higher magnitude indicates higher error.
The feature-feature correlations maintain the same overall pattern as the original data,
though some features like age aren't as strongly tied to the rest.
With this, we see that not only has Reformer modeled each feature distribution, but
it has also modeled all the feature dependencies. This is what makes Reformer, among
other things, very effective at running simulations and generating good synthetic data.
When used to train a new model for predicting heart disease diagnosis and testing on real, held-out data, we see the performance hold up within a few points of what the real data would render:
(Real Dataset Results)
test_accuracy : 0.742 (0.811)
test_roc_auc : 0.847 (0.859)
test_average_precision : 0.832 (0.860)
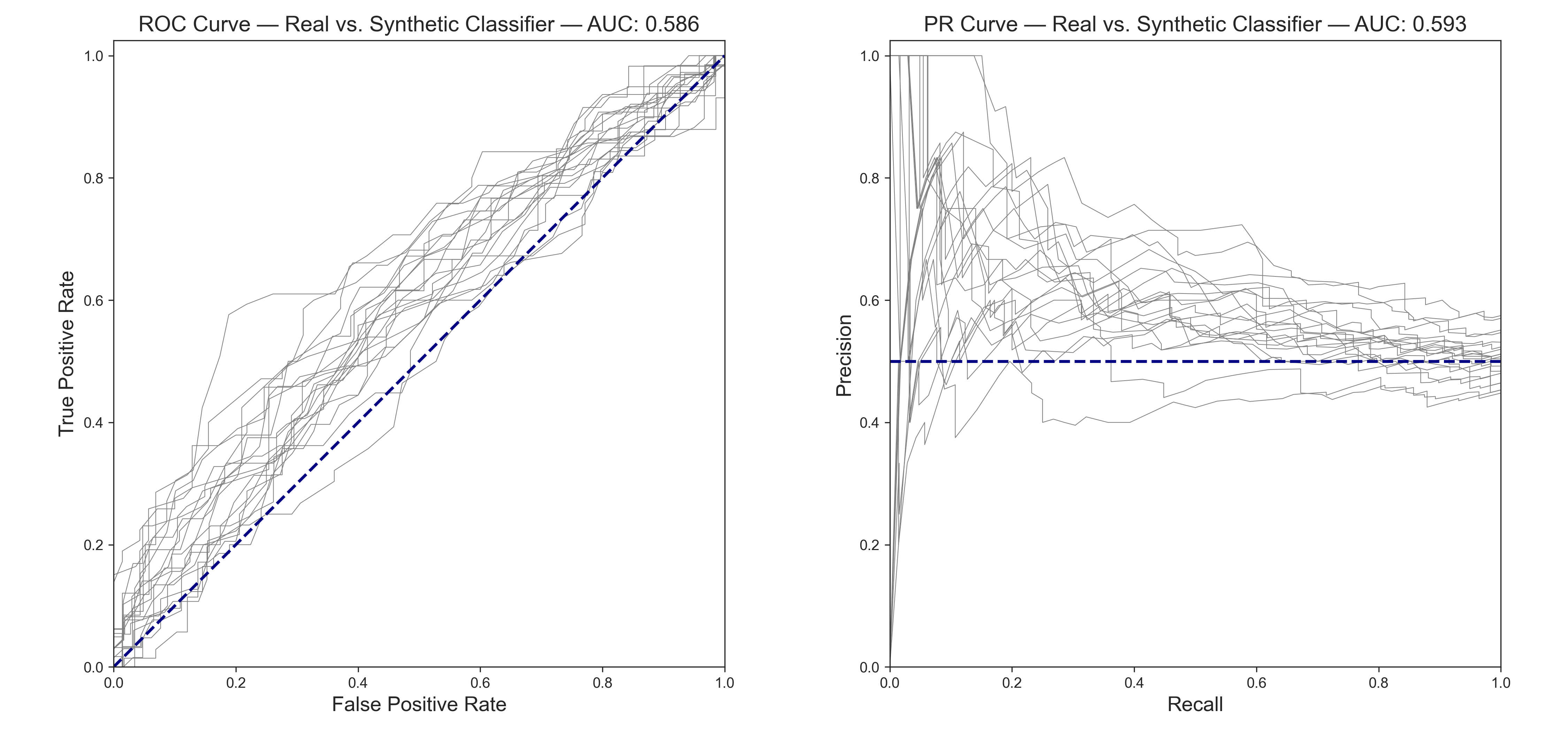
A classifier model cannot tell the real from the synthetic very well at all (ROC and PR AUC < 0.6). Also, observe that the curves are much closer to the 0.5 lines, indicating better indistinguishability than the CTGAN-based model.
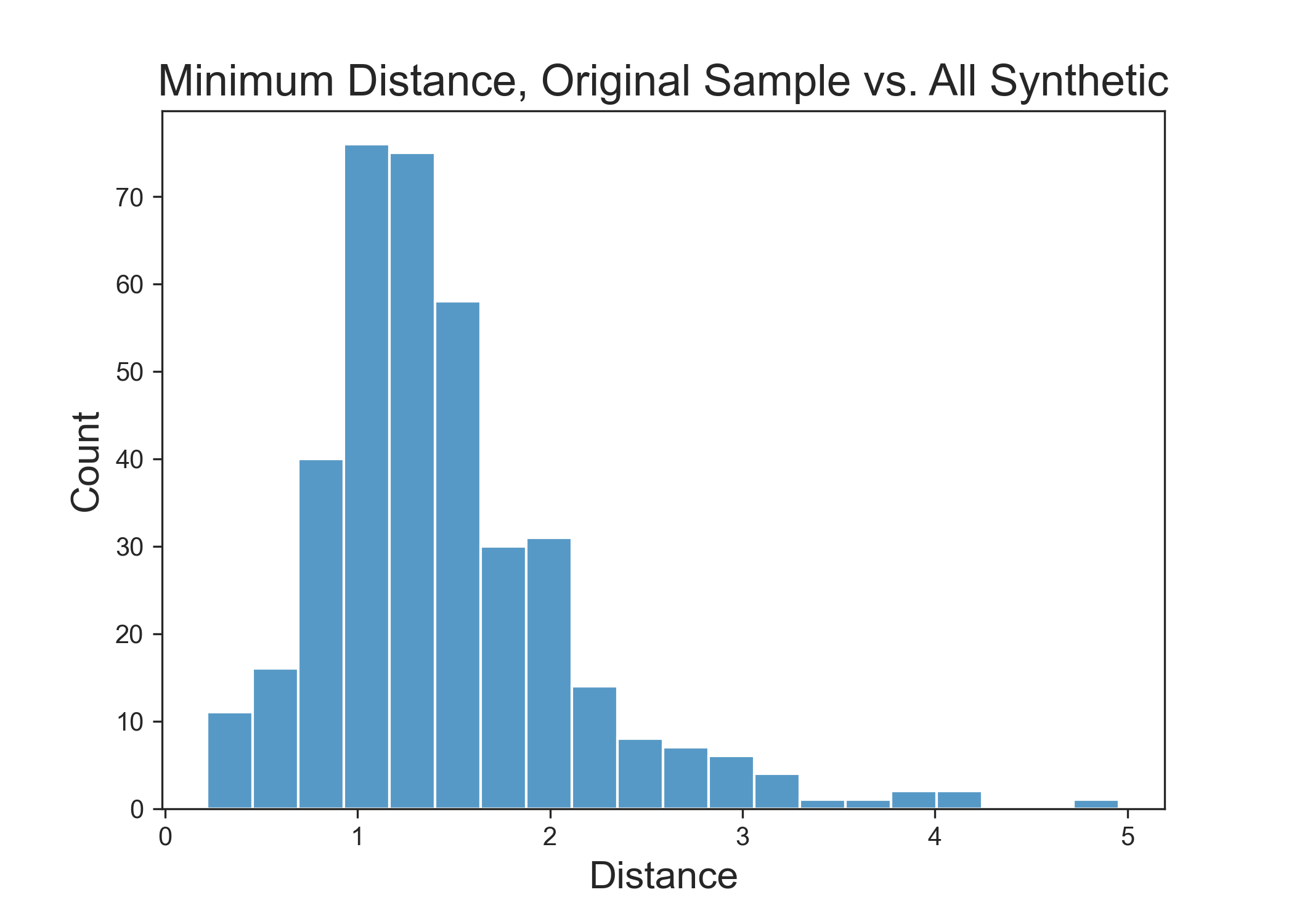
Above: Distance between real data and Reformer synthetic data. Lower numbers indicate values that are more like the original data. Distance of 0 indicates synthetic data that are identical to real data.
Again, while maintaining the model utility and distributions that the real data has, we see that there are no real samples that have snuck into our synthetic dataset. This can be seen with the gap in the minimum distance plot around zero.
| Dataset | Sum(|Δcorr|) | Diagnosis ROC AUC | Diagnosis PR AUC | Diagnosis Accuracy | Real vs. Synthetic ROC AUC | Real vs. Synthetic PR AUC | Real vs. Synthetic Accuracy |
|---|---|---|---|---|---|---|---|
| Real | N/A | 0.859 | 0.860 | 0.811 | N/A | N/A | N/A |
| CTGAN | 2.26 | 0.865 | 0.867 | 0.774 | 0.804 | 0.807 | 0.727 |
| Redpoll Reformer | 2.19 | 0.847 | 0.832 | 0.742 | 0.586 | 0.593 | 0.562 |
Finally, we summarize these results comparing the performances of CTGAN against Redpoll Reformer. While CTGAN does maintain more of the original dataset's predictive power for the heart disease diagnosis task, we see that Reformer's synthetic data is much more indistinguishable from the original dataset (Real vs. Synthetic results). Likewise, the structure of the dataset is also more accurately maintained, as can be seen when the absolute differences in feature-feature correlation values are summed up (smaller is better).
It should be understood that Redpoll's Reformer is primarily designed to help the user understand and utilize their data. To this end, Reformer purposefully generalizes, tending to prioritize the big picture over the few niches, nooks, and crannies of the data. As a result, Reformer will sacrifice a few points of task-specific accuracy in favor of the many benefits of generalization.
Final Word
This is one aspect of what Reformer can do by learning and modeling the information in a dataset. The data simulated by Reformer:
- Requires no feature transformation: Can handle numeric, categorical, and missing values
- Matches the original data structure: Individual and joint distributions are maintained
- Maintains privacy: No synthesized samples completely match real samples
- Nearly indistinguishable from real data: Even a classifier struggles to tell the two apart
- As effective at modeling: Synthesized data maintain the utility of the original data set